Screenshots of the
Programming Examples
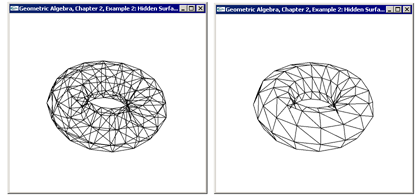
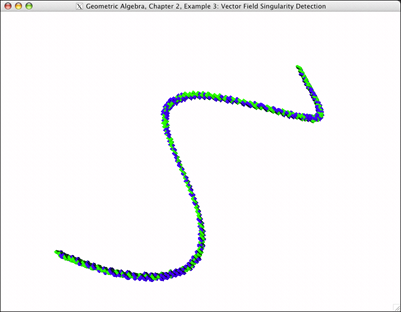
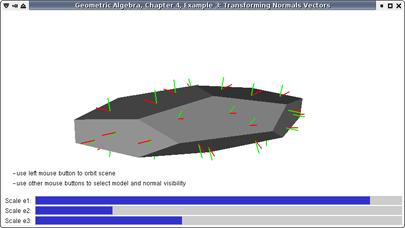
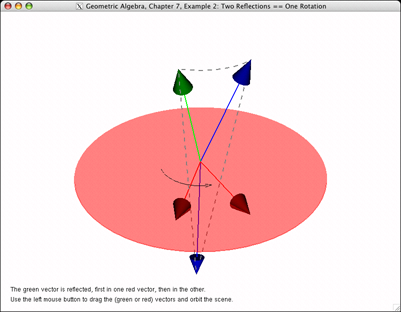
These are screenshots of the programming examples of Chapter 1 through 16. Most screenshots have been reduced in size to fit on the page. Click to see them in full resolution.

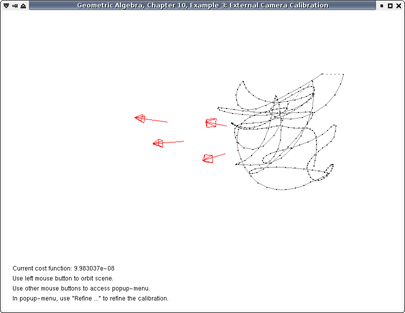
Chapter 10, Example 3: This example shows how to compute the external calibration of cameras. The external calibration is the relative position and orientation of cameras. The calibration is performed by waving a single marker through the volume of space visible to the cameras. The cameras register the position of the marker on each frame, and use this to find a rough initial estimate of their position and orientation. A geometric algebra based algorithm is then used to optimize this estimate.
The four cameras are shown as pyramids with a line extending to indicate their viewing direction. The marker measurements are shown as black dots with a line connecting them.